I will be covering both Data Structures and Algorithms
- Data Structures (including Abstract) - Arrays, Lists, Stacks, Queues, Hashtables, Trees, Heaps, and Sets
- Algorithms - Search (Linear and Binary), Sort (Bubble, Selection, Insertion, Shell, Merge, Quick, Counting and Radix) and Recursion
Data Structures can organize and store data, there are many types of data structures each can be used for a specific requirement, there are some guidance on what algorithms to use but testing the application is always recommended.
Algorithms are steps to perform a specific task, remember an algorithm is not the implementation but the steps, the code is the implementation. Again there could be many algorithms that do the same thing but testing will make sure which one is the best solution.
In order to measure the performance of an algorithm there are two steps that are involved
- Number of steps a algorithm uses, we look at the worst case (time complexity)
- Amount of memory used to complete the steps, not so much of an issue now days (memory complexity)
Using the example of adding sugar to a cup of tea, the number of steps increases the more sugars you want (right-hand screenshot) and thus the time complexity also increases.
 |
 |
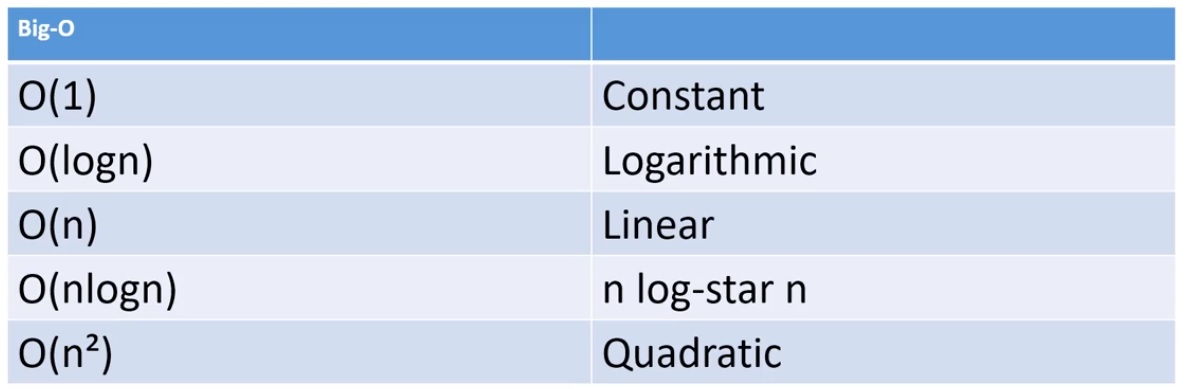
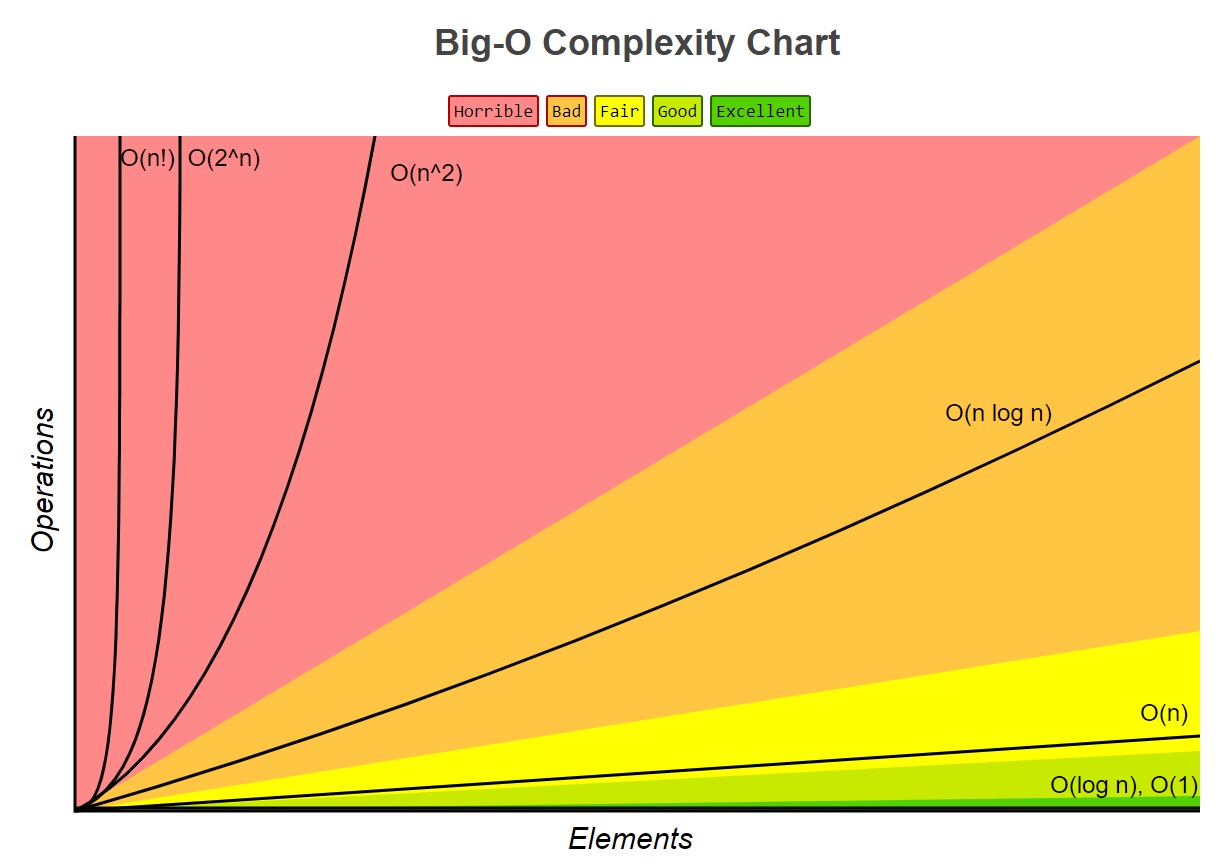
The big-O notation for the above is 2n + 2, the 2 is steps 1 and 2 and care constant, but steps 3 and 4 depends on the number of sugers (n) so we get 2n, we can see that the steps are linear. The are many big-O values but at basic level we would be using the below without getting to complex. The table below starts with the best time complexity to the worst time complexity. Although you might not really use Big-O notation when developing its still good to have a little understanding of it when picking an algorithm, you would pick the best time complexity algorithm first and then test. There are many graphs on the internet which represent the Big-O notation, this is a good URL as it includes both data structures and algorithms.
 |
 |
Arrays are one of the simplest types of data structures, they are not dynamic meaning that once created you cannot grow/shrink an array. The index starts a 0, arrays are storage in one continous block in memory, each element is the same size which is the same of the object stored, so for example int whould be 4 bytes each.
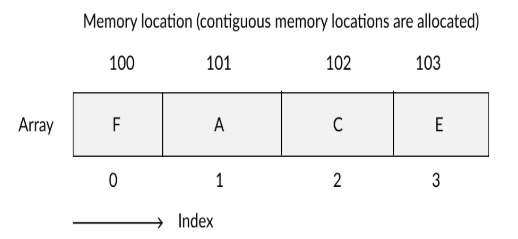
Java uses the formula x + (i * y) to get the memory address of the element, this means we can get to any element very quickly even if there are millions of elements, there are 3 steps to retrieve no matter how many elements which means this is O(1) which is constant time complexity, so its very quick if you know the element/index. However if you need to search the array it has to traverse the array, worst case would be we have to search the whole array and thus the more elements the more steps, this means it would be O(n) linear.
| Arrays | int[] intArray = new int[7]; // an array that holds 7 integers (index 0-6)
intArray[0] = 10; // start address for example is 20
intArray[1] = 20; // 20 + ( 1 * 4 bytes ) = 24
intArray[2] = -30; // 20 + ( 2 * 4 bytes ) = 28
intArray[3] = 40; // 20 + ( 3 * 4 bytes ) = 32
intArray[4] = 50; // 20 + ( 4 * 4 bytes ) = 36
intArray[5] = 60; // 20 + ( 5 * 4 bytes ) = 40
intArray[6] = -70; // 20 + ( 6 * 4 bytes ) = 44
for(int i=0; i < intArray.length; i++) {
System.out.println(intArray[i]);
} |
The Big-O notation for an array is below:
| Operation | Time Complexity | Performance |
|---|---|---|
| Retrieve with Index | O(1) - constant time | excellent |
| Retrieve without index | O(n) - linear time | good (depending on size) |
| Add an element to a full array (create new array and copy) | O(n) | good (depending on size) |
| Add an element to the end of an array | O(1) | excellent |
| Insert and Update an element at a specific index | O(1) | excellent |
| Delete an element by setting it to null | O(1) | excellent |
| Delete an element by shifting elements | O(n) | good (depending on size) |